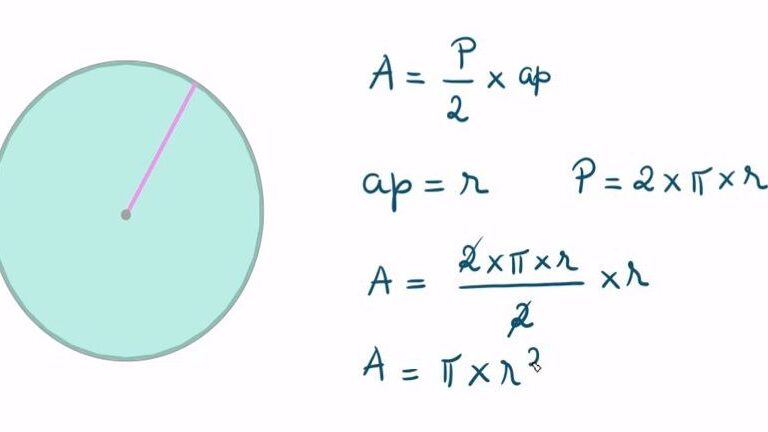Exemplos de como calcular a área de um círculo passo a passo

Você já parou para pensar na importância de entender como calcular a área de um círculo? Essa habilidade é fundamental em diversas áreas, desde a matemática até a engenharia e o design. Neste artigo, vamos explorar exemplos de como calcular a área de um círculo de forma simples e prática, tornando esse conceito acessível para todos.

Exemplos De Como Calcular Área De Um Círculo

Para calcular a área de um círculo, utilizamos a fórmula A = π * r², onde A representa a área e r é o raio do círculo. Vamos explorar alguns exemplos para ilustrar esse cálculo de forma clara e fácil de entender.

Exemplo 1: Círculo com Raio de 3 cm

1. Identificamos o raio: r = 3 cm.
2. Calculamos a área: A = π * (3)².
3. Resolvemos a equação: A = π * 9.
4. Aproximamos π: 3,14 * 9 = 28,26 cm².
5. Área do círculo: 28,26 cm².

Exemplo 2: Círculo com Raio de 5 m

1. Identificamos o raio: r = 5 m.
2. Calculamos a área: A = π * (5)².
3. Resolvemos a equação: A = π * 25.
4. Aproximamos π: 3,14 * 25 = 78,5 m².
5. Área do círculo: 78,5 m².

Exemplo 3: Círculo com Diâmetro de 10 cm

1. Convertendo diâmetro para raio: r = 10 cm / 2 = 5 cm.
2. Calculamos a área: A = π * (5)².
3. Resolvemos a equação: A = π * 25.
4. Aproximamos π: 3,14 * 25 = 78,5 cm².
5. Área do círculo: 78,5 cm².

Exemplo 4: Círculo com Raio de 1,5 m

1. Identificamos o raio: r = 1,5 m.
2. Calculamos a área: A = π * (1,5)².
3. Resolvemos a equação: A = π * 2,25.
4. Aproximamos π: 3,14 * 2,25 = 7,07 m².
5. Área do círculo: 7,07 m².

Exemplo 5: Círculo com Raio de 0,8 m

1. Identificamos o raio: r = 0,8 m.
2. Calculamos a área: A = π * (0,8)².
3. Resolvemos a equação: A = π * 0,64.
4. Aproximamos π: 3,14 * 0,64 = 2,01 m².
5. Área do círculo: 2,01 m².

Esses exemplos destacam como calcular a área de um círculo de maneira prática e acessível. É fundamental praticar com diferentes valores para aprimorar a compreensão do conceito.

Fórmula Para Cálculo Da Área

A fórmula para calcular a área de um círculo é simples e eficiente. Utilizamos a equação A = π * r², onde “A” representa a área, “π” (pi) é aproximadamente 3,14, e “r” é o raio do círculo.

O Que É A Área De Um Círculo

A área de um círculo é a superfície contida dentro de seus limites. Representa o espaço ocupado pela figura circular.

• Relação com o raio: A área varia com o quadrado do raio, o que significa que pequenas mudanças no raio podem resultar em grandes variações na área.
• Importância em aplicações: A área é fundamental em diversas áreas, como construção, design e planejamento urbano.
• Medições comuns: Pode ser expressa em diferentes unidades de medida, como centímetros quadrados (cm²) ou metros quadrados (m²).

Como Utilizar A Fórmula

Usar a fórmula para calcular a área de um círculo é direto. Aqui está um passo a passo prático.

• Identificar o raio: Determine o valor do raio do círculo. Se tiver um diâmetro, divida-o por dois para encontrar o raio.
• Calcular o quadrado do raio: Multiplique o raio por ele mesmo (r * r).
• Multiplicar por π: Multiplique o resultado obtido pelo valor de π (use 3,14 ou uma calculadora para um valor mais preciso).
• Interpretar o resultado: O valor final resultará na área do círculo, apresentada na unidade de medida correspondente.

Exemplos Práticos

Vamos aos exemplos práticos de como calcular a área de um círculo. Esses exemplos ilustram o processo e facilitam a compreensão do conceito.

Exemplo 1: Círculo Com Raio Conhecido

Calcular a área de um círculo com raio conhecido é simples. Utilizamos a fórmula (A = π times r²). Consideramos um círculo com um raio de 3 cm:

Agora, um segundo exemplo, usando um círculo com raio de 5 m:

Exemplo 2: Círculo Com Diâmetro Conhecido

Quando temos o diâmetro, fazemos uma conversão para obter o raio. Utilizamos a fórmula (A = π times r²). Consideramos um círculo com diâmetro de 10 cm:

Assim, esses exemplos demonstram como calcular a área de um círculo, utilizando tanto o raio direto quanto a conversão do diâmetro.

Dicas Para Facilitar O Cálculo

Para tornar o cálculo da área de um círculo mais simples e eficiente, podemos seguir algumas dicas práticas. Essas orientações ajudam a evitar erros e garantem que consigamos realizar os cálculos de forma precisa. Vamos conferir:

• Use uma calculadora científica. Essa ferramenta facilita a multiplicação por π, evitando erros aritméticos.
• Conheça o valor de π. O número π é aproximadamente 3,14, mas também pode ser utilizado como 3,14159 para mais precisão.
• Trabalhe com unidades consistentes. Utilize sempre a mesma unidade de medida para o raio e, consequentemente, para a área.
• Verifique a conversão de unidades. Quando necessário, converta o raio em centímetros ou metros antes de realizar o cálculo.
• Desenhe o círculo. Visualizar a figura ajuda a compreender a relação entre o raio e a área, facilitando o aprendizado.
• Pratique com diferentes raios. Quanto mais exemplos diferentes realizarmos, melhor será nossa compreensão do conceito.
• Faça anotações. Registrar os passos do cálculo pode ajudar a consolidar o entendimento e identificar erros comuns.

Seguindo essas dicas, o processo de calcular a área de um círculo se tornará mais acessível e descomplicado. As práticas constantes e a atenção aos detalhes são fundamentais para garantir confiança nos resultados obtidos.

Conclusão

Calcular a área de um círculo é uma habilidade essencial que podemos aplicar em diversas situações do nosso dia a dia. Compreender a fórmula A = π * r² e praticar com exemplos variados nos ajuda a dominar esse conceito.

Ao utilizarmos dicas práticas como o uso de calculadoras e a verificação de unidades, conseguimos evitar erros comuns e garantir resultados precisos. A prática constante é a chave para nos sentirmos mais confiantes e seguros ao realizar esses cálculos.

Portanto vamos continuar explorando e praticando, pois a matemática está presente em muitos aspectos da nossa vida e saber calcular a área de um círculo é apenas o começo.